In today's post we featured this pin:
.jpg) |
| http://themetapicture.com/the-japanese-way/ |
It took me a while to figure out what they did, but it's awesome. We've had some requests to explain how to do this and make it work, so using my super high tech Microsoft Paint program, I'll walk you through how to do this multiplication trick.
We'll start with multiplying single digits together. We'll do 3x4. I tried to "color code" each number (I'm sorry to those with color blindness, like my husband...the colors won't help a whole lot, I know).
Start with the first number, 3. Draw 3 vertical lines.
Next, go to your second number, 4. Draw 4 horizontal lines across the vertical lines you just drew.
Now, you are looking for the intersections of the lines (where they cross):
Count all the intersections, and you have your answer:
So now, what about multiplying numbers with double digits?
Let's look at the problem in the original pin, 13 x 12.
Let's look at the problem in the original pin, 13 x 12.
Start with the first digit of the first number. In this case that's the 1 of the 13. Draw 1 vertical line.
Now move on to the second digit in the first number. That would be the 3 of the 13. Spaced to the right of your first vertical line, draw 3 vertical lines grouped together.
Now let's move to 12. Take the first digit of the second number. That would be the 1 of the 12.
Draw 1 horizontal line at the top.
Then take the second digit of the second number. That's the 2 of the 12. Spaced below your first vertical line, draw 2 vertical lines grouped together.
Now, we need to group the intersections. We do this in diagonals from the top left corner, working down to the bottom right corner. Circling the groups helps keep everything all in place in your head. See the graphic below:
Each circle/oval counts as one group.
Now we count up the intersections for each group we just circled in the previous step.
Working clockwise around the drawing gives you your answer. Always start at the upper left corner and then follow the numbers in sequence. 1, 5, 6. 13 x 12 = 156
Let's look at another double digit problem. Start by making you vertical lines to represent your first number in the problem.
Add the horizontal lines for your second number.
Circle your groups.
Count up the intersections in each group.
Now here's where this one changes a little. The answer to 15 x 23 is not 21315. When you run into a problem that produces groups that have intersections in the double digits (like the 13 and the 15 in this problem). You have an extra step you have to take.
Start with the first double digit grouping in your drawing. In this case that's the 13. You are going to take just the first digit (the 1) and add it to the group directly to the left (the 2). See the brown underline I did in the graphic below. Write the sum of the two numbers above the drawing. I find it easy to draw lines from the numbers to their sum so I know for sure what numbers are referring to.
Still working with that 13, we are now going to take the 3 and add it to the first digit of the next number working clockwise around the drawing. So we end up with 3 + 1 (see the numbers I have underlined in purple in the graphics below).
At this point it may be easy to cross out the numbers you used to add up to your new numbers. Was that clear as mud? Here:
Now that you have just single digit numbers around your drawing, you have your answer. As before, start with the first number and work clockwise around the drawing: 3, 4, 5. 15 x 23 = 345
And finally I'll show triple digit multiplication. Start by drawing the vertical lines for your first number.
Draw the horizontal lines for your second number.
Circle the groups. Remember, you group them together in diagonals.
Count up the intersections in each group.
Then starting with the first number and working clockwise you have your answer.
This method can be used for any whole number multiplication problem.
3 x 28
11 x 121
1,985,343 x 3,546 (but for that one I'd just recommend getting a calculator)
Just remember the first number gets vertical lines, the second number gets horizontal lines, and group in diagonals.
I hope this made some sense. If not, let me know and I'll try again to explain it.









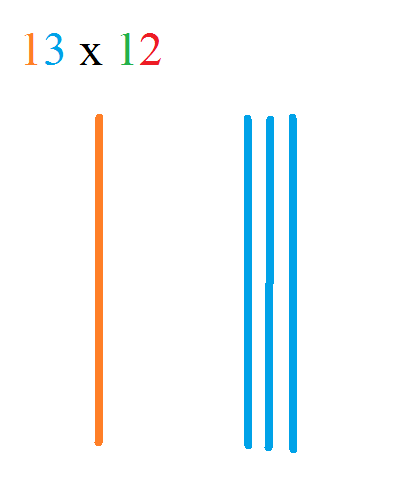



















I'd worked all this out earlier - I can't look at something like that without at least *trying* to figure out how and why it works.
ReplyDeleteI'd agree with you on all points except the 'working from the left' bit. This method takes any multiplication problem and turns it into an addition sum. I always work from right to left in addition and so did the same here (both working it out and writing it down right to left). This made the whole 'carrying the one' bit far clearer and more natural.
Isn't it a lot easier to just multiply the regular way, in a column? Same principle, less useless lines.
ReplyDeleteI'm sure that depends on how you were taught to do it as a kid. Whatever you're already used to is usually easiest as an adult.
DeleteI find it is easier to do the "normal" column method, but this method might work really well for my brother who has discalculia (dislexia but with numbers). Multiplication doesn't click for him as normally taught, but something like this might make it possible for him to figure it out. Next time I see him I'm going to see if this makes any sense to him.
DeleteNo. Just nope. Columns and numbers, please! Lol!
ReplyDeleteI went to figure it out right away and really had a good time with it. I found the carrying easier if you do the first number with the horizontal lines, second number with the vertical. Thanks for bringing this to my attention.
ReplyDeleteIsobel says this looks a lot like something that Miro would paint. ;O)
ReplyDeleteI'm curious to know how you would do a problem like 568 X 586. Once you group them together diagonally you have 5 groups and one of those groups contains a 3 digit number. I tried to wrap my brain around it but gave up. Although, I am still curious to know how that works.
ReplyDeleteI think I have it figured out; let's see if I can explain it just in words (you might have to do the problem as I explain for it to make sense). I ended up with grouping numbers of (starting at top and moving around clockwise) 25, 80, 124, 96, and 36. To figure this one out I ended up using Jenn's tip to work right to left (or counter clockwise) starting with the last number, which for this particular problem would be the 36. I circled the 6 so I'd know that was my final single digit. Then I took the 3 and added it to the 6 of the 96. Then I took the 9 of the 96 and added it to the 4 of the 124. Then I took the 12 (as they were the remaining numbers) of 124 and added it to the 0 of 80. I added the 8 of 80 to the 5 of 25. And that left the 2 single. So then here were the numbers I had left, starting at the top and working CW: 2, 13, 12, 13, 9, 6. Again, I started at the bottom number and worked my way back up Counter Clockwise. The 6 and 9 I left alone because they were already single digits. You then take the 3 off the 13 and make it a single digit in the sequence (so the last three numbers of the final answer will be 396). Take the 1 of the 13 and the 2 of the 12 and add them together. Take the 1 of the 12 and add it to the 3 of the 13. Take the 1 of the 13 and add it to that first 2. Finally you have all single digits and your answer, 343,396.
DeleteHowever 568x586=/=343396 it equals 332,848. I tried it using the method shown on this page and first got 3,329,048. Then i went back and checked my numbers and realized i miss counted some of the intersections, I think its easier to count the lines that are about to intersect vertically and horizontally then multiply as opposed to counting the intersections themselves which can be difficult when you get higher up.
DeleteAnyway i got it right using the same way as for the smaller problems. I found it helpful to number what digit place each grouping is after you count all the intersections. For example in this problem the furthest right number is 48 so i numbered 8 as the first digit and 4 as going to be the second digit in the answer. Anyways i still got it to work.
Thankyou for teaching me this wonderful method, I'm a college student currently and am taking some applied calculus classes. I found it as a helpful more fun method, maybe just because its new. Also i found it funny some people said they liked the multiplying columns method easier. Well i tried to do that method for 212x121 and realized i dont remember how to do it anymore. i realize that may sound silly but i rarely dont use a calculator anymore and now i have this method i may not return to the columns, anyway thanks again for taking the time to teach me this.
For me, in lieu of adding the digits it makes more sense after getting the totals in the grouping to start at the right and each going around goes from the ones, tens, hundreds, thousands, etc. So in the 15x23 you ended up with 2, 13 and 15 so starting at the right you have 15 ones, 13 tens (=130) and 2 hundreds (200) thuse 200+130+5=345. In the 121×212 you had 25652 so obviously that's easier but to break down from right to left 2 ones, 5 tens, 6 hundreds, 5 thousands and 2 ten thousands. That's essentially what it's saying anyway because it really is the same as our column multiplication as it is multiplying the digits via the intersecting lines. May help others to see it that way to understand why it works.
ReplyDeleteUmm, not for me. I learned the old school way and that's how I teach my kiddoes. This gave me a headache!
ReplyDeleteThis is great! I'm going to show it to my 10 year old niece that has petite mal epilepsy. She has a hard time in school and I really think this is going to help her! Thank you so much for sharing this
ReplyDeleteDo you understand how much this could help those with visual processing disorders? AH! I'm so excited to have found this and I'm going to try it and use it in the kids I tutor as well as show it to the school board to see if we can use it as an alternative for those with special needs. I am also thinking of how great it would be to use pipe cleaners to give them a way of manipulating it until they "grasp" the idea and can move forward with the "traditional" column math style. Thank you so much!
ReplyDeleteI am very thankful calculator has been invented.
ReplyDeletewhats the real name of the method you are using ? plss
ReplyDeleteI don't know what this method is called, when I found the pin with this it didn't have any name attached to it.
Delete